Nixon 帶你玩數學
基礎數學題:64是否等於65?
Mathematics丨STEAM丨Illusion
你和平常一樣走在回家的路上,見到不遠處聚集了一些群眾,很是熱鬧。「大概是街頭表演或 者宣傳活動吧?不理了我只想快點回家。」 身體加快了腳步,但目光還是禁不住好奇心下意識的投向 嘈音的來源。你看見一個街站、一個神態自若的男人,身邊有一群他的狂熱信眾,不斷重覆的叫嚷: 「64=65! 64=65! 64=65! 64=65!」

這位文質彬彬的瘋子引領你到街站跟前,剛才坐著的男人收起了世不恭的笑容並拿出四塊拼 圖。他用溫柔而肯定的語氣問道:「你知道矩形、三角形、和梯形的面積計算方法嗎?」你輕點一下頭,他把拼圖拼成以下形狀:
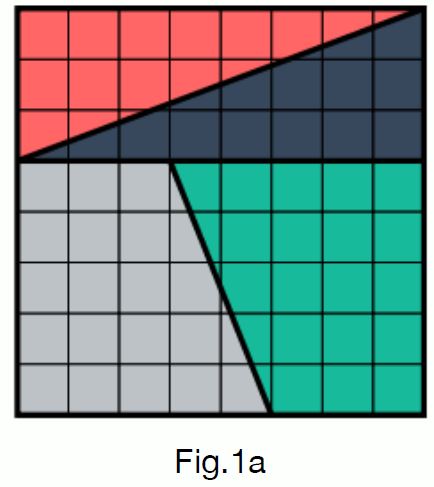
「非常好。接下來我把這四塊拼圖稍為移動一下,這個新圖形的面積是多少?」
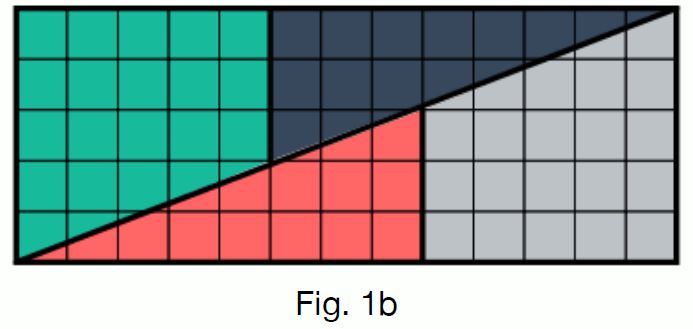
「這個長方形的長度是 5+8,闊度是5,面積是13×5 = ... 65 sq. units?怎可能?這是甚麼回事?」
男人依舊是那個表情,似乎對你的驚訝反應丁點也不覺得意外,亦不打算替你釋疑,就像看好 戲一樣端起他的咖啡,靜坐一旁觀賞着你的表演。
「(3+5)×5÷2 = 20、3×8÷2=12、長方形面積是 20+12+12+20 = 64,但又等如 65 …」
「5×(8+5) = 65 但又等於 64,是真的有可能嗎?」
你口中唸唸有詞,腦袋瘋狂轉動,不斷來回驗算嘗試找出不妥之處,可惜一無所獲。
「怎可能一個長方形的面積是 64 同時又是 65?這不科學!你到底藏起了什麼機關?」
未等男人反應你就把拼圖搶了拿在手上,但半天都未能發現任何異樣。正如你所見,它們只是兩對很 普通的直角三角形和梯形。
經過不斷毫無進展的反覆思索,你發覺腦袋已被掏空,已經不能再想出任何可能性。不,還有 一個,一個你曾經認為只是瘋言瘋語,你絕不想承認的嶄新觀點:
「或許 … 在某種特殊情況,64 真的可以等於 … 65 …?」
你視線開始往左右兩邊游移,這是尋求協助的眼神。可是你眼中只有一個場景:一個街站、一 個神態自若的男人,身邊有一群他的狂熱信眾,不斷重覆的叫嚷:64=65! 64=6! 64=65! 64 =65! 在一片重疊叫喊聲籠罩中,忽然你靈光一閃!
「原來如此!我早就該察覺到!這樣說來一切就講得通了!」你暗自讚嘆自己的聰明,在這個 關鍵的瞬間竟然發現了真相!你如獲至寶,提高嗓門準備大聲宣告,恨不得把所有蒙在鼓裏的蒼生喚 醒:
「根本毋庸置疑!64 就是 65!65 即是 64!64=65!」
故事沒有結局,只是狂熱的人群多添了一個新成員。
「64=65」
故事暫告一段落,讓我們回歸主題。
65當然 ≠ 64,聰明的讀者可能早已洞悉當中奧妙:
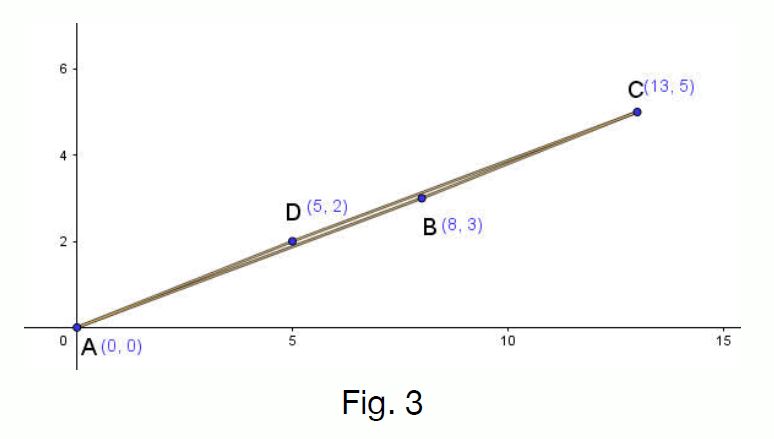
Q.1 Show that area of parallelogram ABCD is 1 sq. unit.
證明平行四邊型 ABCD的面積是一平方單位。
Determinant of a Matrix 矩陣的的行列式:
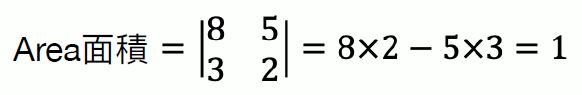
Area面積 = 13×5 − [(3+5)×5÷2 + 3×8÷2]×2 = 1
可是就這樣一個數學趣味分享未免太簡單。Nixon的數學專欄豈止如此?接下來才是主菜:
1. 那個空隙能不能變更大或更小?
2. 還有沒有更多類似的 Puzzle?
3. 更進一步,我們能否自己創作 Missing Square Puzzles?
答案是 Yes! We can! 而製作 消失方形拼圖 的關鍵材料是 ......
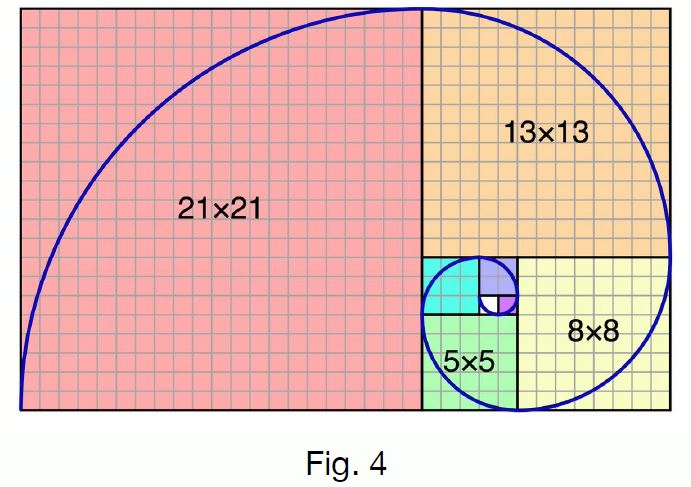
Fibonacci Numbers 費波那契數
意不意外?驚不驚喜?為何是它?
公式是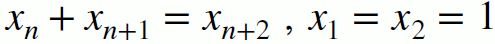 。
。
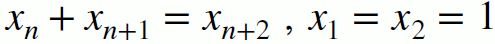 。
。而神奇地,
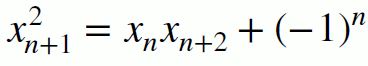 ,
例如 8² = 5×13 - 1、 13² = 8×21 + 1, 可理解成
,
例如 8² = 5×13 - 1、 13² = 8×21 + 1, 可理解成「邊長為 費氏數 的正方形的面積 與 長闊分別為 其前一個後一個費氏數的長方形的面積 相差 1」
只要拼圖中 三角形的底、三角形的高=梯形的上底、梯形的下底=其高 是 連續的 Fibonacci Numbers, 我們便能創作屬於自己的 Missing Square Puzzle!
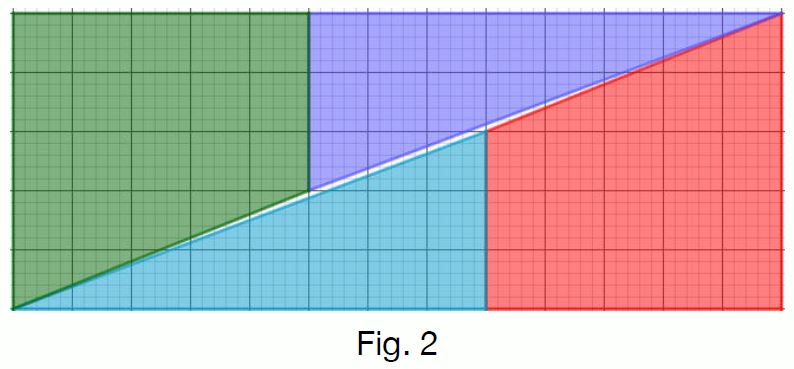
這是我用 8、13、21 製作的示範:
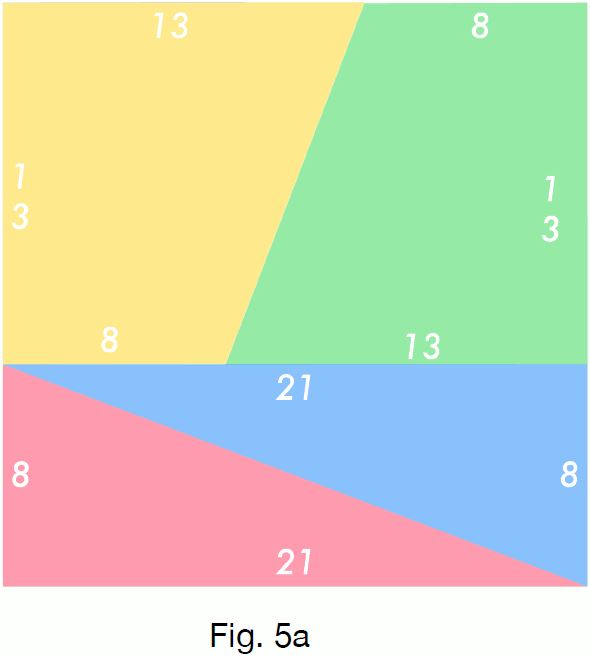
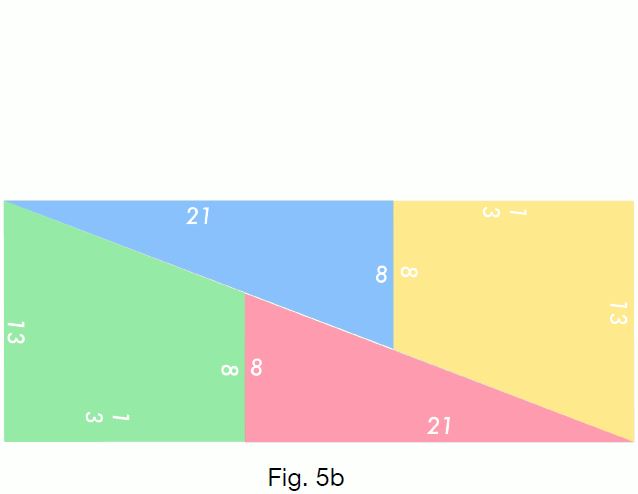
希望您和我一樣喜歡本期內容,我們下期再見!
Nixon Chan
• 香港大學數學系榮譽畢業, 十年正式教學經驗
• 曾出版獲獎數學練習,現為英皇教育數學科名師
• 主力教授香港高中數學,兼教國際課程包括 IBDP、GCE(A-level)、SAT
• 教學宗旨為「沒有弱學生,只有錯方法」,熱衷鑽研「易學且有效」的解題法及計數機程式
文章來源《星島日報 教育版 專欄》- Nixon Chan








